Nix by example
This is a copy of the [1] published 2014 and updated at 2019 (Archive).
Nix is a package manager. ‘Nix’ is also the name of the programming language that it uses. The language can actually be used independently, without any package management at all. Here I show the Nix expression language by example. My approach is to introduce expanding subsets of the language: at any point you can stop reading and have a full understanding of the subset introduced up to that point.
I’ll assume you’ve already installed Nix. Next stop, hello world! From the terminal, run:
$ nix-instantiate --eval --expr '"Hello world"' "Hello world"
What happened here? Nix took the expression "Hello world", evaluated it, and printed out the value. This means that the following is a valid Nix expression:
"Hello world"
and, since it is already a value, the result of evaluating it is exactly the same string:
"Hello world"
Notice that we did not tell Nix to print the string. Explicit output is not part of the language. In fact, there are no commands at all. You cannot write to a file or call an external command. There is no way to read input. The only thing that happens is evaluation of an expression to a value. Think lambda calculus, not Java.
The expression language introduced so far is extremely simple:
Expression ::= String String ::= '"' StringChar* '"' StringChar ::= Space | Alphanumeric
Notice strings are enclosed in double-quote characters! Using single-quotes will give you an error:
$ nix-instantiate --eval --expr "'Hello world'"
error: syntax error, unexpected invalid token
at «string»:1:1:
1| 'Hello world'
| ^
Special characters
So far, the string expressions we’ve seen evaluate to a list of alphanumeric characters and spaces. But in general, a string is a list of unicode code points. We must learn how to write those code points in string expressions.
For example, I haven’t yet taught you how to write a literal double-quote in a string. Using a plain double-quote will result in a confusing error:
> "He said "Hello world""
error: undefined variable 'Hello'
at «string»:1:11:
1| "He said "Hello world""
| ^
Instead, we use the backslash as the escape character.
> "He said \"Hello world\"" "He said \"Hello world\""
Notice Nix uses the same encoding in its output. To encode a literal backslash we use two backslashes:
> "Write \\\" to write a literal double-quote" "Write \\\" to write a literal double-quote"
Thus our grammar expands to:
StringChar ::= '\\' | '\"' | Space | Alphanumeric
The backslash is used to encode many characters:
| Sequence | Encodes character | Unicode code point |
| \n | line feed | 10 |
| \t | tab | 11 |
| \r | carriage return | 13 |
| \\ | backslash | 92 |
Primitive types and operators
The expression we gave Nix was really just a value — in particular, a string. Nix knows about other standard kinds of values:
$ nix-instantiate --eval --expr '42' # integers 42 $ nix-instantiate --eval --expr 'true' # booleans true
The only primitive numeric type is the integer. Nix has no ‘floating point’ or rational types — apparently, package management just doesn’t call for anything except integers.
Nix also has familiar operators to manipulate those values. Here are some examples, which are also our first examples of real evaluation:
$ nix-instantiate --eval ––expr '"Hello " + "world"' "Hello world" $ nix-instantiate --eval ––expr '2 + 3' 5
Standard stuff: + is a binary operator which concatenates strings or adds integers. By this point, we can use Nix as a simple desk calculator:
$ nix-instantiate --eval ––expr '(400 + 2) * (-5) + (5 * 30)' -1860 $ nix-instantiate --eval --expr '(4 * 4 * 4) < (5 * 5 * 5)' true
Addition is easy; let’s try division:
$ nix-instantiate --eval --expr '2/3' /Users/jhf/dev/nix/2/3
Hmm. Not what you expected? That weird answer is because Nix interprets the expression as a path, and I’ll explain that later. For now, just get used to being liberal with whitespace:
$ nix-instantiate --eval --expr '2 / 3' 0
This division operator sure is tricksy! Remember I said Nix only has integers? Because integers are not closed under division, Nix has to do integer division (rounding towards zero).
REPL
From now on, I’ll omit the nix-instantiate command and pretend we’re in a REPL, like this:
> (4 * 4 * 4) < (5 * 5 * 5) true
If you want a real REPL, you can run:
$ nix repl nix-repl> 4*4*4 < 5*5*5 true
Errors
We saw that the + operator works on both strings and integers. Hmm … can we mix strings and integers?
> "Hello" + 6 error: cannot coerce an integer to a string, at (string):1:1
… nope. Unlike some crazy languages, Nix correctly tells us that a string added to an integer is a stupid. Sharp-eyed readers will notice I lied earlier when I said that the only thing that happens is ‘evaluation to a value’. Actually, one of two things happen: either evaluation terminates with a value, or aborts with an error. An error signals a mistake by the programmer, and there are several kinds of mistakes we’ll see which result in such errors. You can also generate errors explicitly with the abort builtin:
> abort "Just not feeling it today" error: evaluation aborted with the following error message: `Just not feeling it today'
Errors are fatal: if anything evaluates to an error, the entire program stops. You cannot ‘catch’ an error. (Although we will see later that Nix also has exceptions, which can be caught.)
Typing discipline
When we made the mistake of adding a string to an integer, the type error that Nix gave us was a runtime type error, not a compile-time type error. We did not annotate our expression with a type declaration, and Nix did not attempt to infer a type for it before doing evaluation. Nix has no type-checking phase (though there are plans for static typing) or any user-facing notion of compilation; it jumps straight to evaluation. You can call it dynamic, if you like.
Nix is able to give us sensible runtime type errors like this because values are tagged with their type, as in many other scripting languages. Before performing the + operation, Nix checks the tags of the values. If they are both strings, it concatenates them; if they are both integers, it adds them; else it aborts with an error.
Nix also exposes these tags to the program via the typeOf builtin:
> builtins.typeOf "foo"
"string"
> builtins.typeOf (2 + 2)
"int"
> builtins.typeOf ("foo" + 2)
error:
… while evaluating a path segment
at «string»:1:26:
1| builtins.typeOf ("foo" + 2)
| ^
error: cannot coerce an integer to a string: 2
And for each type T, there is also a convenience isT builtin:
> builtins.isInt (2 + 2) true > builtins.isBool "true" false > builtins.isBool false true
Even though Nix is dynamically typed, it can help to describe expressions with types. Where it helps, I’ll write annotations like:
# 6 : int # builtins.isInt : any -> bool # builtins.isInt 6 : bool # builtins.typeOf : any -> string
Function application
You have seen some builtin functions such as abort and typeOf. The syntax for function application simply uses whitespace. The argument does not require parentheses around it, though it doesn’t hurt:
> builtins.isInt 4 true > builtins.isInt(4) true
All the functions we have seen take a single argument. Now let’s look at one that takes two arguments. Integer division is available as a builtin function:
> builtins.div 10 5 2
We write the function name followed by all the arguments in order, all separated by whitespace. Parentheses are not necessary, but they can help to show how the expression is parsed:
> (builtins.div 10) 5 2
If this doesn’t look familiar, read it carefully. I lied when I said that div ‘takes two arguments’. Actually, functions in Nix always take exactly one argument, and multi-argument behavior is achieved via currying. That means that builtins.div is a function which takes an int, and returns another function, which in turn takes another int and finally returns the value.
This means that we don’t have to provide all the arguments at once:
> builtins.typeOf (builtins.div) "lambda" > builtins.typeOf ((builtins.div) 10) "lambda" > builtins.typeOf (((builtins.div) 10) 5) "int"
Just like in lambda calculus, functions in Nix are first-class values. The expression ‘builtins.div 10’ gives us a first-class function value, which we can pass around in our program in the same way we pass around integers and strings. Following ML, I would write the static type of builtins.div like this:
# builtins.div : int -> int -> int
You should mentally parse the -> as right associative, i.e.:
# builtins.div : int -> (int -> int)
Function definition
We can define our own functions by writing anonymous function literals. The syntax is slightly unusual, though. Let’s write a function to square an integer:
> x: x*x # int -> int <LAMBDA>
This is the same as (λx. x*x) in lambda notation, or function(x){return x*x;} in JavaScript. The x before the colon is the name of the bound variable, and the x*x after the colon is the returned expression. Our function value is just like the builtin functions:
> builtins.typeOf (x: x*x) "lambda"
We can apply an integer argument to our function to get its square:
> (x: x*x) 3 9
(By the way, since we now have abstraction and application, we have the lambda calculus, and so Nix is clearly Turing-equivalent.)
Earlier I said that functions of multiple parameters can be defined via currying. Let’s define a function which takes two integers and returns the sum of their squares. This does not actually require any new syntax:
> (x: y: x*x + y*y) # int -> int -> int <LAMBDA> > (x: y: x*x + y*y) 3 7 58
Parse trees and evaluation order
And now for some excruciating detail! Parentheses make it clearer how this expression is parsed:
((x: (y: (x*x + y*y))) 3) 7
We can draw this expression — and in fact every Nix expression — as an abstract syntax tree. The tree for the above expression is shown below.
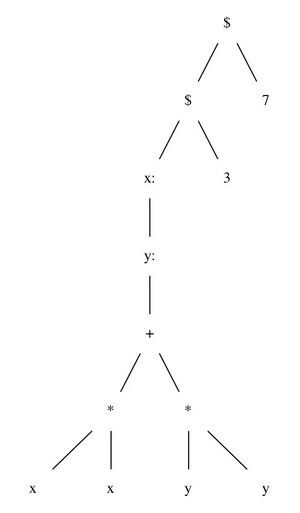
In these diagrams, nodes labelled ‘$’ represent an application of the function on the left to the value on the right. A node labelled ‘x:’ represents an abstraction, binding the name x. A node labelled x or y is a variable. Other nodes are primitive operators.
Evaluation reduces this tree to the single value: 58. This is achieved by repeatedly transforming the tree into a new tree until the tree is just a single value. We can understand the Nix expression language just by understanding each evaluation step as a function from trees to trees.
Each step starts by looking at the top node of the tree. In the example, this is ‘$’, an application. To do an application, Nix first needs to reduce the left child to a function, so it looks at the left child. The left child is another application, so the same logic applies: look at the left child. This time, it’s a function ‘x:’, so we can apply it to the right child, the value ‘3’. Function application means substitution of all references to the bound variable, ‘x’, with a reference to the function argument, ‘3’. This yields a new, simpler tree:
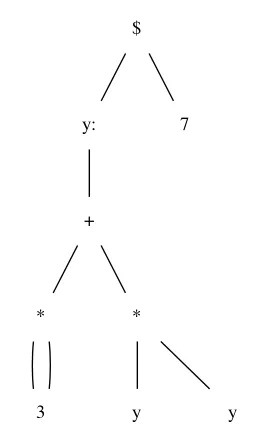
(Alright, I lied again. Strictly speaking, these aren’t trees, since the value ‘3’ has two parents. At the moment, this is not important.)
We say that this step forced the left child. Forcing a subexpression means evaluating it until its top node is a data-type, like an integer, string, or function. The left child was forced to obtain a function which could be applied to the right child, ‘7’.
We have a new tree, and the process starts again. This time, the left child is a function, so we can do another function application: substitute all occurrences of ‘y’ with the value ‘7’.
Now the top node is the + operator. Just like function application forces the left child until it is a function, the + operator forces the left child until it is a string or an integer. Forcing the left child here is easy: Nix knows how to multiply 3*3, so we substitute the value 9. After that, the + operator forces the right child, which is just as easy: Nix knows how to multiply 7*7, so we substitute 49.
Here’s the entire process in glorious detail!
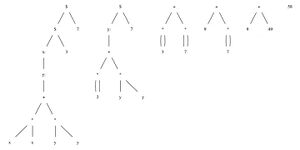
We can express the same reduction textually like this:
((x: (y: (x*x + y*y))) 3) 7 # initial expression (y: (3*3 + y*y)) 7 # substitute x=3 3*3 + 7*7 # substitute y=7 9 + 7*7 # multiplication 9 + 49 # multiplication 58 # addition
So, why have I gone into such detail here? First, because many languages you’re used to can’t be expressed in this way — their execution state is better expressed as statements, with a stack, and a heap. In contrast, the execution state of the Nix expression language is the same as its abstract syntax tree, like lambda calculus.
Second, because it shows Nix’s evaluation order: evaluation in Nix always looks at the top of the tree, where other languages look at the leaves first. We say that Nix is lazily evaluated, where other languages are strictly evaluated. This distinction was not important here, but will become important later: laziness allows for excellent decoupling in our programs, and it is also key to Nix’s efficiency.
Let expressions
Our sum-of-squares implementation does not use our squaring function, which is a shame. We didn’t do so because it’s not obvious how to name our squaring function in such a way that we can refer to it from our sum-of-squares implementation.
Technically, we can achieve naming and reuse with the features we have so far, by passing in the squaring function as an argument to the whole expression:
> (square: (x: y: square x + square y) 3 7) (x: x*x) 58
However, a much more idiomatic way of writing the last example is with a let expression:
> let square=(x: x*x); in (x: y: square x + square y) 3 7 58
The let expression has two parts, let <bindings> in <body>. The bindings are a series of definitions separated by semi-colons; in this case we bind our function to the variable square. The body of the expression can then reference square.
Notice that the only way to define a ‘named function’ in Nix is to assign an anonymous function to a variable. There is no special syntax.
Detour: evaluating files
Our Nix expressions are getting a bit complex for a single line. To write larger expressions easily, we can write them in a file. Create a file called squares.nix with the content:
let # square : int -> int square = x: x*x; # sumOfSquares : int -> int -> int sumOfSquares = x: y: square x + square y; in sumOfSquares 3 7
Nix (mostly) ignores whitespace, so this is the same expression as in the previous example. Now, back in the shell, run:
$ nix-instantiate --eval squares.nix 58
From now on, I’m going to write multi-line Nix expressions and their result like this:
let square = x: x*x; sumOfSquares = x: y: square x + square y; in sumOfSquares 3 7 ==> 58
Notice that I added the sumOfSquares function to the let bindings, and that it references the square binding. Bindings in the same let expression can refer to each other.
Conditionals
Our Nix expressions are starting to look like real programs! We only need one more thing: the conditional. Let’s define an function to give us the absolute value of an integer. Enter the if-then-else operator:
let
# abs : int -> int
abs = x:
if x < 0 then (-x)
else x;
in
abs (-3)
==> 3
Notice that if-then-else is an expression, not a statement: the whole expression evaluates to either the if-branch or the else-branch depending on whether the condition is true or false. Again, there are no statements in Nix. A reminder on how Nix is evaluating an expression like this one:
(x: if x < 0 then (-x) else x) (-3) # initial expression if (-3) < 0 then (-(-3)) else (-3) # function application if true then (-(-3)) else (-3) # do less-than operator (-(-3)) # do conditional 3 # do negation
Boolean operators and laziness
You’re probably familiar with “short-circuiting” boolean operators in most languages. Nix has those, too. You can understand the semantics of boolean operators as syntactic sugar for if-then-else expressions, which shows when the operands are evaluated:
Operator expression Equivalent to ! A if A then false else true A || B if A then true else B A && B if A then B else false A -> B if A then B else true
(Oh, that last one looks unusual? It’s just the implication operator you’re familiar with from propositional logic. For some reason, most programming languages don’t include it, but Nix does. It’s particularly useful for assertions, which we’ll meet soon.)
We can test when the right-hand operand is evaluated by using abort:
> false && (abort "hmm") false > true && (abort "hmm") error: evaluation aborted with the following error message: `hmm'
You can try it yourself with the other operators.
Recursion
Now we have conditionals, we can write interesting recursive functions with base cases. Since we can encode the lambda calculus, we could write recursive functions using the Y combinator! This is unnecessary, though, because let expressions in Nix already allow recursion. The factorial function can refer to itself:
let
# factorial : int —> int
factorial = n: if n == 0 then 1
else n * factorial (n — 1);
in
factorial 5
==> 120
Recursion in let expressions is really just a special case of the fact that bindings can refer to each other: they can refer to themselves, too.
Loops?
Yeah … nope. Ain’t no loops around here. Loops only make sense in a language with mutability, which Nix doesn’t have. We do everything with good old-fashioned recursion. For example, you can write the Fibonacci function using a helper function with an ‘accumulator’:
let
# fib' : int -> int -> int -> int
fib' = i: n: m: if i == 0 then n
else fib' (i — 1) m (n + m);
# fib : int -> int
fib = n: fib' n 1 1;
in
fib 30
==> 1346269
Composite data-types and laziness
And now for something completely different.
All the data-types we have seen so far have been primitive data-types. But for complex data, we’d like composite data-types. For this, Nix gives us ‘sets’. Sets might be more familiar to you as ‘maps’ or ‘objects’. A set is just key-value pairs, where the keys are strings:
> { "name" = "james"; age = 26; }
{ age = 26; name = "james"; }
The key-value pairs have no special ordering; Nix happens to show them in alphabetical order. Be sure not to confuse the braces with ‘code blocks’, and be sure not to confuse the key-value pairs with assignment statements! They are not statements, they are not ordered, and the keys are not mutable. Also be sure not to confuse sets with object-oriented ‘objects’; there are no ‘methods’, no hidden state, and no ‘subtype’ relationships; there is nothing more to a set than its keys and values.
Let’s do some more evaluation. Am I definitely 26 years old? I shouldn’t have to work it out; let’s make Nix do the work:
> { age = 2014 — 1988; }
{ age = < CODE >; }
Wait, what the heck does ‘< CODE >’ mean? Instead of showing us ‘26’ like we were expecting, Nix didn’t bother doing the subtraction at all. Whaa?
Remember when we talked about Nix’s evaluation order? Evaluation of our program is equivalent to simply forcing the entire expression, and Nix stops forcing as soon as the top node is a data-type. Well, a set is a data-type, so it stops, and doesn’t do any more evaluation ‘inside’ the set. So expressions like ‘2014 – 1988’ are left unevaluated because they were not required in order to determine the outermost data-type.
Okay, how do we ‘solve’ this laziness thing? One way is to just turn on strictness:
$ nix-instantiate --eval --expr --strict '{ age = 2014-1987; }'
{ age = 27; }
Another way to do the same thing using nix-repl is to use the :p command:
nix-repl> :p { age = 2014-1987; }
{ age = 27; }
(Yet another way to do the same thing from within the language is to use builtin.deepSeq on the expression, but that was only implemented this week!)
Another way is to extract the age value from the set. Meet the dot operator:
> { age = 2014–1987; }.age
27
Now Nix is forced to evaluate the subtraction expression because it is the top-level value. We can view the evaluation as a series of steps from the initial expression to the final value:
{ age = 2014–1987; }.age # 1. initial expression
2014–1987 # 2. do the dot operator
26 # 3. do the subtraction operator
Notice the order of steps 2 and 3. Most other languages would have done it in the opposite order. For example, here’s JavaScript:
{ age: 2014–1987 }.age # 1. initial expression
{ age: 26 }.age # 2. do the subtraction operator
26 # 3. do the dot operator
Where most languages would do the outermost operation last, Nix does it first! As soon as the outermost thing is no longer an operator but a data constructor (like string, integer, or set), it stops. So now you know why Nix didn’t bother doing our subtraction in the first example.
Lists
We could use sets to encode lists using a linked-list structure. However, Nix gives us another basic composite data-type for lists. We can write a literal list as a whitespace-separated list of other expressions, all in square brackets:
> [1 (1+1) "three"] # list any [ 1 < CODE > "three" ]
Note the absence of commas between the list elements. Note also that we can freely mix the types of the elements; integers and strings in the same list poses no problem. (It’s not great style, though.)
Just as with sets, the list elements are left unevaluated unless they are forced. To extract an element from a list, we can use a built-in function called builtins.elemAt. This function has two parameters, a list and an integer, and returns the value in the list at that index:
> builtins.elemAt [1 (1+1) "three"] 1 2
Nix provides many builtin functions for manipulating sets and lists. Some self-explanatory examples:
> builtins.attrNames { age = 26; name = "james"; }
[ "age" "name" ]
> builtins.tail [1 2 3 4 5]
[ 2 3 4 5 ]
> builtins.head [1 2 3 4 5]
1
> [1 2 3] ++ [4 5 6]
[ 1 2 3 4 5 6 ]
Infinite data structures
Nix’s laziness makes it easy to define data structures which are conceptually infinitely large. Streams are a well-known example: the Fibonacci sequence is a stream of integers. Let’s try defining the Fibonacci sequence in Nix as an infinite list.
let # fibsFrom : int -> int -> list int fibsFrom = n: m: [n] ++ fibsFrom m (n+m); # fibs : list int fibs = fibsFrom 1 1; in builtins.elemAt fibs 30 ==> segmentation fault
Yeah … again, I lied to you. Nix lists are not actually the lazy linked lists known to functional programmers. They are arrays, with a strict finite length. The segmentation fault was a stack overflow caused by builtins.elemAt trying to fully evaluate the infinite list before doing anything else.
But we can instead implement streams using sets, which are lazy. Let’s represent a stream as a two-element set: one element called head, which is the first element of the stream, and another element called tail, which is the rest of the stream encoded as another two-element set.
# type stream a = U nil { head=a; tail=stream a; }
let
# streamElemAt = s: i:
if i == 0 then s.head
else streamElemAt s.tail (i - 1);
fibsFrom = n: m: {
head = n;
tail = fibsFrom m (n + m);
};
fibs = fibsFrom 1 1;
in
streamElemAt fibs 30
==> 1346269
Lazy loopiness and recursive sets
Nix’s laziness also allows us to write extremely declarative definitions. An example. I am 26. My father is 28 years older. My father’s surname is “Fisher”. My surname is the same as my father’s. Given these facts, we can define both of us as Nix sets:
let
james = { surname = dad.surname; age = 26; };
dad = { surname = "fisher"; age = james.age + 28; };
in
{ james = james; dad = dad; }
==(strict evaluation)==> {
dad = { age = 54; surname = "fisher"; };
james = { age = 26; surname = "fisher"; };
}
What devilry is this? Is Nix using some kind of constraint solver? Actually, no; it’s just using laziness and substitution! The james and dad value get repeatedly substituted until there is just addition and attribute lookup to do.
Nix gives us a way to express this even more compactly using recursive sets. These are just like normal sets, except the keys are in scope in the values. The syntax is that for normal sets, preceded by the keyword rec:
rec {
james = { surname = dad.surname; age = 26; };
dad = { surname = "fisher"; age = james.age + 28; };
}
You can understand the recursive set notation as syntactic sugar for a recursive let-expression. That is, the recursive set above is the same as the let expression before it.
Modules, public and private
We previously defined a streamElemAt function which worked like builtins.elemAt but for streams. It would be nicer to build a ‘module’ called streams to contain generic functions like this, so we could refer to it as streams.elemAt, just like we refer to builtins.elemAt.
The key thing we need when writing a module is a way to expose a public interface while keeping implementation details private. We don’t need any new tools for this; just a let expression. The expression let <bindings> in <body> allows us to define some private bindings and expose a public body. Put this in a file called streams.nix:
let
cons = head: tail: { head = head; tail = tail; };
iterate = step: head: cons head (iterate step (step head));
map = f: {head, tail}: cons (f head) (map f tail);
elemAt = l: i: if i == 0 then l.head
else elemAt l.tail (i - 1);
in {
iterate = iterate;
map = map;
elemAt = elemAt;
}
We’ve defined a new module! It exposes three public functions: iterate, map and elemAt. It keeps another function, cons, as a private implementation detail.
Imports and paths
But how can we access this new module? Since it’s just another expression, we can just embed it in every file we want to use it in. But a nicer way is to use an import to allow us to keep the streams module in a separate file.
First we need a way to specify the file to import. Instead of using bare strings to represent the filepath, Nix has a dedicated primitive data-type for this. Paths are written as bare filepaths, and they evaluate to themselves:
> /etc/passwd /etc/passwd > builtins.typeOf /etc/passwd "path"
You can also write relative paths. From the shell, these are resolved relative to the current working directory:
> ./foo.nix /Users/jhf/dev/nix/foo.nix
Always include the dot at the start! Paths have to have at least one slash for Nix to recognize them as paths rather than variables:
> foo.nix error: undefined variable `foo' at (string):1:1
(This, by the way, explains why Nix does not have an infix division operator: the slash character is reserved for paths.)
A relative path is resolved relative to the file in which it occurs:
> ./streams.nix /Users/jhf/dev/nix/streams.nix
Relative path resolution happens at parse time, not runtime. It is not possible to pass around relative paths in the program to be resolved at some later time. Paths in the language are always absolute paths.
Now just put the word import before a path, and you’ve got yourself an import expression! If our file streams.nix is as before, then we can import it in fib.nix to use its elemAt function:
let
fibsFrom = n: m: {
head = n;
tail = fibsFrom m (n + m);
};
fibs = fibsFrom 1 1;
in
(import ./streams.nix).elemAt fibs 30
==> 1346269
The import expression simply evaluates to the Nix expression in the imported file. Notice, as always, that the import is an expression, meaning it can go anywhere any other expression can go.
The substitution of the file contents for the import expression happens lazily, just like all other expressions. This means the file is only loaded when the import expression is forced. If your program does not force the import, the file is not loaded.
The only (sensible) constraint is that the imported Nix expression must not contain any free variables; it is an error for the imported expression to try to use anything defined in the file doing the importing.
Circular imports
Most other languages will complain if you write two modules which import each other. Thanks to laziness, you can get away with these so-called ‘circular imports’ as long as your definitions are not truly circular. Let’s take our father/son example from earlier, and put them in separate files. Here’s james.nix:
{ surname = (import ./dad.nix).surname; age = 26; }
And here’s dad.nix:
{ surname = "fisher"; age = (import ./james.nix).age + 28; }
Now from the REPL we can run:
> { james = import ./james.nix; dad = import ./dad.nix; }
{ dad = { age = 54; surname = "fisher"; }; james = { age = 26; surname = "fisher"; }; }
No errors! There are no errors because, just as when the content was all in the same file, there is no true circularity in our definitions.
Dynamic scope
If you’ve used JavaScript, you might have seen its with statement. It’s widely regarded as a design mistake, and it was removed from the language in ES5 strict mode. Well, you’ll be pleased to learn that with makes a reappearance in the Nix expression language! Whether this is also a mistake is up to you.
As usual, with in Nix creates an expression, not a statement. It takes a set S, and another expression E, and puts the values of the set S in scope when evaluating the expression E. It’s really only used for importing modules, putting all the utilities in the module into scope. Let’s try it with our Fibonacci program:
with (import ./streams.nix);
let
fibsFrom = n: m: {
head = n;
tail = fibsFrom m (n + m);
};
fibs = fibsFrom 1 1;
in
elemAt fibs 30
==> 1346269
Notice that we did not have to provide a fully-qualified name for the elemAt function, as it was injected into scope. Just be aware that it makes your program a bit harder to reason about, so use it judiciously.
Multi-parameter functions using sets
You saw previously how to define multi-parameter functions using currying. Another way is to put all the parameters in a set and pass that as the single argument. So these are alternative definitions for sum-of-squares:
> (x: y: x*x + y*y) 3 7
58
> (args: args.x*args.x + args.y*args.y) {x=3; y=7;}
58
This second form is more verbose, but it’s useful when defining functions with lots of arguments. It’s used often enough that Nix provides support for it as set patterns. The following is just syntactic sugar for the previous:
> ({x, y, ...}: x*x + y*y) {x=3; y=7;}
58
Now, instead of binding the argument to a single variable, we bind the keys of the argument set as multiple variables in the function body.
The ellipsis at the end of the pattern tells Nix to allow other unused keys in the argument. If you want stricter behavior where those extra arguments are an error, then remove the ellipsis:
> ({x, y}: x*x + y*y) {x=3;y=7;z=9;}
error: anonymous function at (string):1:2 called with unexpected argument `z’, at (string):1:1
Default arguments
You’ve probably used a language with ‘default arguments’. The idea is to allow the function caller to omit some arguments, where the omitted arguments are replaced with default values defined by the callee.
If you use a set to represent multiple arguments in Nix, then you can emulate this behavior verbosely using builtins.hasAttr. If for some reason you wanted the arguments to sumOfSquares to default to zero if not provided, we could write:
(args:
let
# builtins.hasAttr : string -> set -> bool
x = if builtins.hasAttr "x" args then args.x else 0;
y = if builtins.hasAttr "y" args then args.y else 0;
in (x * x) + (y * y)
) {x=3;}
==> 9
Another way to emulate this behavior is with Nix’s set union operation, written set1 // set2. It takes two sets and evaluates to another set which contains the union of the keys in the input sets, and takes the values from the right-hand set in the event of a clash. We can therefore put our default arguments in the left-hand side set:
(args':
let args = { x=0; y= 0; } // args'; # // is not a comment!
in (args.x * args.x) + (args.y * args.y)
) {x=3;}
==> 9
But since this is such a common pattern, Nix provides syntax sugar for it as the name ? e pattern:
> ({x ? 0, y ? 0}: (x * x) + (y * y)) {x=3;}
9
Exceptions
All of the errors we’ve seen so far have been fatal errors: they cause the entire program to abort. But in addition to these fatal errors, Nix also has exceptions, which can be ‘caught’ by a caller. Exceptions can be created explicitly using the throw builtin:
> throw "I'm an exception" error: I'm an exception
Here, our exception was not caught, and so it was shown as an error. We can catch the exception using another builtin called tryEval:
> builtins.tryEval (throw "I'm an exception")
{ success = false; value = false; }
The tryEval builtin takes an expression, forces it, and if it throws an exception, returns the set shown above. If the expression evaluates to a value without any exceptions, the returned set contains the value:
> builtins.tryEval (2 + 2)
{ success = true; value = 4; }
Note that tryEval only catches exceptions, not errors. If the argument generates an error, it’s a fatal error, just like before:
> builtins.tryEval (abort "I'm an error") error: evaluation aborted with the following error message: `I'm an error'
Assertions
Many other languages have an assert statement: you provide it a boolean expression, and if it evaluates to false, an exception is thrown. We use it to ensure at runtime that preconditions are satisfied before continuing.
Nix has a very similar feature, the assert expression:
> assert (2 < 1); "icecream" error: assertion failed at (string):1:1 > assert (1 < 2); "icecream" "icecream"
We provide it with two expressions: a boolean check and the expression to evaluate if the check passes. In the first example, because 2 < 1 evaluates to false, the entire expression throws an exception. In the second example, because 1 < 2 evaluates to true, the entire expression evaluates to the second value, “icecream”.
Note the semicolon between the check and the body. We can chain assertions together in a way that looks a lot like statements, but as always are just more expressions:
let
max = x: y:
assert builtins.isInt x;
assert builtins.isInt y;
if x < y then y
else x;
in
max 5 "six"
==> error: assertion failed
Since the assertion failure is an exception rather than an error, we can use tryEval to catch the assertion failure:
let
max = x: y:
let
attempt = builtins.tryEval (
assert builtins.isInt x;
assert builtins.isInt y;
if x < y then y
else x
);
in
if attempt.success then attempt.value
else throw "max : int -> int -> int";
in
max 5 "six"
==> error: max : int -> int -> int
Debugging
Compared to traditional languages, debugging in Nix is a bit different. Since everything is an expression, and expressions are evaluated lazily, the concept of a ‘breakpoint’ doesn’t fit here. There are no facilities for ‘stepping through’ the program execution, and there is no IDE to help with it.
The closest equivalent is builtins.trace:
builtins.trace : forall a b. a -> b -> b
This builtin evaluates its first argument and prints it out, then returns its second argument:
> builtins.trace 1 2 trace: 1 2
This is similar to Debug.traceShow in Haskell, or more distantly, console.log and friends in traditional languages. It’s there to make it easier to find out what’s going on deep inside the evaluation of a large expression.
Note that it won’t trace its argument until the entire expression is forced. If the trace expression is never forced, nothing will be traced:
> { foo = builtins.trace 1 2; }
{ foo = < CODE >; }
Note also that the first argument will only be forced to head normal form, so nested expressions will not be forced:
> builtins.trace { foo = 2 + 2; } "foo"
trace: { foo = < CODE >; }
"foo"
This might be frustrating. Really, using assertions liberally is a better strategy than tracing. If you’re tracing in order to see whether some value meets your expectations, you should instead use assert to state your expectations.
Technically, the existence of builtins.trace contradicts my statement that ‘explicit output is not part of the language.’ But it’s better to think of builtins.trace as a hint to the interpreter like a breakpoint, rather than part of the language per se.
Next time …
I’ll be taking a completely different tack, looking at the layout of Nix packages on the filesystem. Stay tuned!
(2019: Okay, I admit it, it’s unlikely you’ll see a part 2.)
(Thanks to Wout Mertens, Colin Putney, and Luca Bruno for comments and corrections.)
